티스토리 뷰
X선, γ선과 같은 전자기파 방사선의 물질과의 상호작용 메키니즘은 하전입자선과는 상당히 차이가 있으며, 전자기파 방사선과 물질과의 상호작용 과정으로는
① 광전효과
② 컴프턴 효과
③ 전자쌍생성
이렇게 3가지가 있다. 전자기파 방사선은 물질 속을 통과할 때 위에서 언급한 3가지 과정에 따라 흡수 또는 산란하여 차츰 에너지를 잃게 되는데, 이 3가지 과정에 대한 자세히 알아보도록 하자.

X선, γ선은 전자기파 종류의 하나이기 때문에 "전자기방사선"이라 부르며, 전자기파 방사는 전장과 자장의 시간적 변화의 공간적인 전달 현상인데, 전자기파는 파동으로서의 성질 뿐만 아니라 입자로서의 성질도 보유하고 있다. 독일의 천재 물리학자 알버트 아인슈타인(Albert Einstein)이 발견한 상대성이론에 따르면 전자기파 방사선과 같이 에너지 E를 가지고 있는 것은 E/c2 와 같은 질량 m을 가지고 있으며, 질량을 갖은 것은 mv와 같은 운동량 p를 갖는다. 광자는 E = hυ 의 에너지를 가지며, 속도는 c = v 이기 때문에, 동시에 p = mv = (hυ/c2) · c = h/λ 의 운동량을 가진다.
전자기파 방사선은 이와 같은 성질을 가지고 있어 방사선이 물질에 부딪히면 물질을 구성하고 있는 원자, 분자는 하전입자선과 마찬가지로 이온화, 들뜨게 되어 전자기방사선은 그 만큼의 에너지를 잃게 된다. 하지만, 전자기파 방사선은 전하를 가지고 있지 않으므로 원자, 분자에 대한 쿨롱력이 미치는 영향이 없기 때문에 물질과의 상호작용 메카니즘도 하전입자선과는 차이가 있다.
전자기파방사선과 물질과 상호작용
1. 광전효과(Photoelectric effect)
전자기 방사선이 물질 근처를 지나가면 그 근방의 전장과 자장이 크게 진동하기 때문에 궤도전자는 강력한 자극을 받게 된다. 전자기방사선 에너지 hυ 가 궤도전자와 원자핵과의 결합에너지보다 높으면 궤도전자는 원자핵으로부터 구속력을 벗어나서 원자에서 뛰어나가게 되는데, 이러한 현상을 광전효과(photoelectric effect)라 한다.

광전효과(photoelectric effect)는 전자기방사선보다 낮은 에너지의 자외선이나 가시광선에서는 일어나는 것을 확인할 수 있다.
(1) 광전자의 에너지
광전효과 현상으로 인하여 원자로부터 뛰어나오게 되는 전자를 광전자 하며, 광전자의 에너지(Eph)는 다음과 같이 식으로 표현할 수 있다.

위 식에 전자기방사선의 에너지가 이온화에너지보다 낮다면, 아무리 강한 전자기방사선이 와서 부딪혀도 광전효과는 일어나지 않음을 확인할 수 있다. 하지만, 들뜸현상은 충분히 일어날 수 있으며, 광전효과가 일어나기 위해서는 최소한의 진동수 보다는 높은 진동수를 가지고 있는 전자기파 방사선이 필요하며, 이러한 진동수를 한계진동수라 한다.
광전효과는 이온화현상으로 하진입자에 의한 이온화현상과는 크게 차이점이 있는데, 하전입자에 의한 이온화는 이온화를 할 때 하전입자 에너지의 일부를 원자, 분자에 주면서 천천히 에너지를 잃는 반면에 광전효과에 의한 이온화현상은 전자기방사선의 에너지는 이온화 에너지와 광전자의 운동에너지로 모두 바뀌어 원자에 흡수된다. 즉, 전자기방사선은 한 번의 광전효과로 인하여 입사할 때 보유하고 있는 모든 에너지를 잃고 소멸해 버린다. 이와 같이 전자기방사선의 에너지가 모두 흡수되어 버린다고하여 광전효과를 광전흡수라고도 한다.
(2) 광전효과의 발생확률
광전효과의 발생확률은 다음과 같다.

여기서 σph 를 광전자 흡수단면적이라 하며, 광전효과가 발생할 확률은 물질의 원자번호가 클수록 크게 증가하고, 전자기방사선의 에너지가 커짐에 따라 갑자기 감소하게 된다.
그리고 전자기방사선의 에너지 hυ가 K각 전자의 이온화에너지 IK와 가까워지면, σph는 갑자기 커지게 된다.
2. 컴프턴효과(Compton effect)
컴프턴효과란 전자기방사선이 원자, 분자 근처를 지나갈 때 광자가 원자의 궤도전자와 충돌하여 전자에 에너지의 일부를 주어 전자를 튕기고 동시에 광자 자신의 에너지는 그 에너지만큼 낮아져서 다른 방향으로 산란되는 현상을 컴프턴(Compton)이라고 한다.
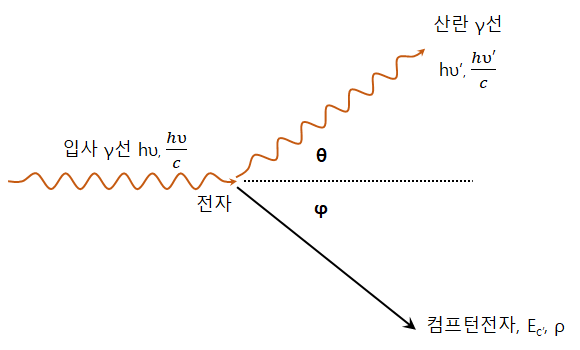
컴프턴효과가 일어나면 궤도전자는 운동에너지를 얻어 튀어 나가고 산란광자의 파장은 길어지고 진행방향도 변하게 되는데, 이렇게 튀어나온 전자를 되튐전자(recoil electron) 또는 컴프톤전자라고 하며, 산란된 전자기방사선은 산란 γ선이라 한다.
컴프턴효과는 전자기방사선의 에너지가 어느 수준까지 높아지면 광전효과보다 일어나기 쉽다. 입사광자의 에너지가 어느 정도 높아지면 궤도전자에 대한 원자핵의 구속력이 상대적으로 무시할 수 있을 정도로 작아지게 되기 때문에 광자와 궤도전자의 충돌에는 원자핵에 의한 결합에너지가 관여하지 않게 된다.
(1) 산란 γ선의 에너지
정지하고 있는 전자 m0 에 에너지가 hυ, 운동량이 hυ/c의 광자가 충돌한 결과 전자는 되튐각 Φ 의 방향으로 광자가 에너지 hυ', 운동량 hυ'/c로 산란되었다면 충돌 전후에 있어 에너지와 운동량은 보존되기 때문에 다음과 같은 식이 성립한다.
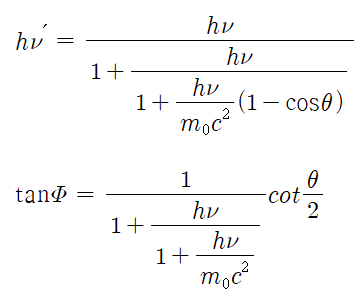
위 식은 산란선의 에너지 hυ' 이 입사광자의 에너지 hυ 뿐만 아니라 산란각 θ 에도 의존하고 있음을 확인할 수 있다.
(2) 되튐전자의 에너지
산란선의 에너지 hυ' 을 구하면 되튐전자의 에너지 Ec는 다음과 같이 쉽게 구할 수 있다.
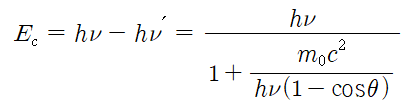
위 식에서 되튐전자의 에너지 Ec는 입사광자의 에너지 hυ 에 비례하여 증가하며, Ec의 최대치는 전자기방사선의 산란각 θ = 180º 일 때, 얻을 수 있으며 그 식은 다음과 같다.
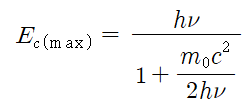
이 식에서 입사하는 입자의 에너지 hυ 가 비교적 낮을 때는, 되튐전자의 에너지는 Ec = 0 으로 되며, 반대로 입사하는 입자의 에너지 hυ 가 높을 때는 Ec(max) ≒ hυ 으로 된다. 따라서, 되튐전자의 에너지는 0에서부터 Ec(max) 까지 분포하는 연속스펙트럼을 갖게된다.
(3) 컴프턴효과의 발생확률
컴프톤효과는 광자와 전자가 에너지보존법칙 및 운동량보존법칙을 동시에 만족시키는 방향으로 산란하고 되튐되는데 그 발생확률과 각도분포는 클라인-니시나(Klein-Nishina)의 공식에 따르며, 이 공식에 따르면, 원자 1개당 컴프턴효과가 일어날 확률 σc 는 다음과 같다.
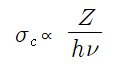
위 식에 따르면, 컴프턴효과의 단면적은 입사광자의 에너지에 반비례하고, 원자번호에 비례함을 알 수 있다.
3. 전자쌍생성
전자기방사선의 에너지가 높아지면 컴프턴효과는 잘 일어나지 않고, 전자쌍생성(pair production) 효과가 일어나는데, 1.02 MeV 이상의 고에너지를 갖는 전자기방사선이 원자 근처를 지나갈 때, 원자핵의 콜롱전장 속에서 광자가 소멸하고, 한쌍의 전자와 양전자가 생성되는 현상을 전자쌍생성(pair production) 이라 한다.
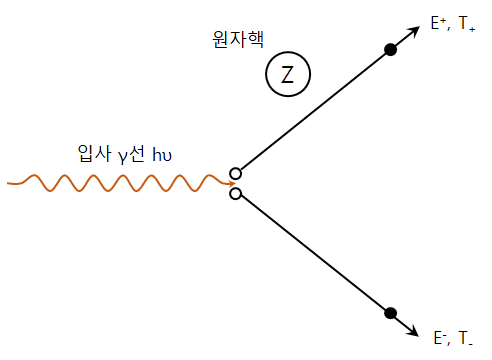
전자쌍생성(pair production) 현상은 자유공간에서는 에너지보존법칙과 운동량보존법칙이 동시에 성립하지 않기 때문에 원자핵의 쿨롱장 내에서만 일어나고 자유공간에서는 일어나지 않는다.
(1) 생성된 전자의 에너지
입사광자의 에너지를 hυ, 전자의 정지에너지를 m0c2, 전자쌍으로 생성된 두 전자의 운동에너지를 각각 E+, E- 라 하면 에너지와 질량 보존법칙에 따라 다음 식이 성립한다.
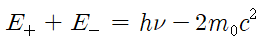
위 식에서 전자쌍생성은 입사광자 에너지의 일부가 두 전자의 질량으로 변하고 나머지는 그 운동에너지로 됨을 알 수 있다. 따라서, 전자쌍생성은 입사광자의 에너지가 전자쌍의 정지에너지 1.02 MeV보다 높지 않으면 일어나지 않는다.
(2) 전자쌍의 발생확률
전자쌍의 발생확률 σpair 은 다음과 같다.
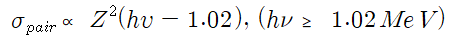
위 식에서 전자쌍생성은 입사광자의 에너지가 높을수록, 또 물질의 원자번호가 높을수록 일어나기 쉽다.
'방사선' 카테고리의 다른 글
| 의료분야 방사선의 중요성과 활용 (0) | 2023.08.11 |
|---|---|
| 방사능 / 방사선장의 계량 / 상호작용계수 (0) | 2023.08.10 |
| 방사선의 역사와 종류 및 방사선에너지 (0) | 2023.08.08 |
| 방사능과 방사성붕괴 (0) | 2023.08.07 |
| 방사성폐기물의 정의, 의료방사성폐기물 특징 및 관리방법 (0) | 2023.08.06 |
- Total
- Today
- Yesterday
